行測數(shù)量關系統(tǒng)籌問題之“排隊取水”
在行測數(shù)量關系的考查中,統(tǒng)籌問題是大家想要去做,但是又做不好的題型。統(tǒng)籌問題題型多樣,但又相互獨立,每類題型都有其核心解題思路,只要把握好解題思路,題目就能迎刃而解。今天江蘇公務員考試網(wǎng)小編就帶著大家學習“排隊取水”問題,讓大家再遇到這類問題能夠很好地解決。
 相關文章
相關文章
什么是排隊取水問題呢?
題型特征:一群人排隊取水,每個人取水的時間各不相同,讓我們計算排隊等待和取水時間總和的最小值是多少。那么我們把這類問題叫做排隊取水問題。
【例1】有A、B、C、D、E5個人去水房打水,分別需要3、5、7、11、15分鐘,若只有一個水龍頭,想5人打水和等待的時間之和最短,則最短時間為多少?
A.91 B.92 C.93 D.94
【答案】C。解析:由問題可知,要求5人打水和等待的時間之和最短。5個人打水的總時間為3+5+7+11+15=41分鐘是不變的。那么,要想總時間最短,只有讓等待總時間最短。而每個人的等待時間等于他前面所有打水人打水時間加和。

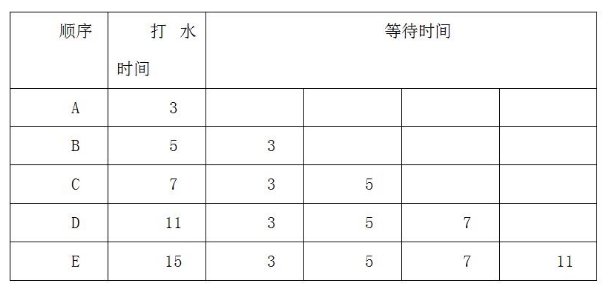
由此可以得出只有打水者速度從快到慢排隊打水,則按照A、B、C、D、E的順序打水才能讓總時間最短。A先打3分鐘,其他四人一共等待了3×4=12分鐘,B打水5分鐘,剩下三人打水共等待了5×3=15分鐘,C打水7分鐘,剩下兩人打水共等待了7×2=14分鐘,D打水11分鐘,最后一人等待11分鐘,所以合計等待時間12+15+14+11=52分鐘。則所求最短時間為41+52=93分鐘。
整理可知:總時間等于3×5+5×4+7×3+11×2+15×1=93分鐘。
這是只有一個水龍頭取水的情況,那如果有兩個水龍頭會是一樣的情況嗎?
【例2】公用電話亭中有兩部電話,六個人排隊打電話,打完即走,他們的通話時間分別為3分鐘、5分鐘、4分鐘、13分鐘、7分鐘、8分鐘,則大家在此公用電話亭逗留的總時間最少為( )分鐘。
A.60 B.66 C.72 D.78
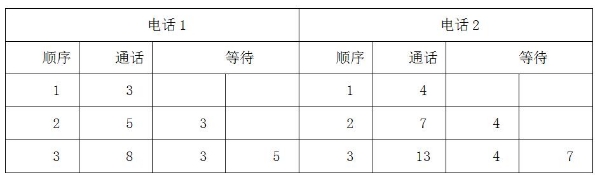
【解析】B。兩部電話可以同時進行,通話時間固定,想讓逗留的總時間最少,就要讓等待時間盡可能少,那就讓通話時間短的人先打電話,六個人按時間從短到長排序:3分鐘、4分鐘、5分鐘、7分鐘、8分鐘、13分鐘,先讓用時最短的兩個人分別去兩部電話(1號和2號),每部電話用完后讓剩下的人中時間最短的接著用,先把六人分成兩組,分配情況如下表:

所求總時間為3×3+5×2+8+4×3+7×2+13=66。
通過上述方法,我們可以發(fā)現(xiàn),排隊取水問題并沒有那么復雜,只需要讓打水時間短的人先打,排好打水順序后確定每個打水時間對應的人數(shù),最后計算出總時間就可以了,希望同學們能夠多加練習,慢慢熟悉此類題型。
 相關文章
相關文章