行測探尋均值不等式的奧秘
數(shù)量關(guān)系是行測考試中讓大家比較頭疼的科目，但其實數(shù)量關(guān)系也有一些比較好做的題型，比如均值不等式。接下來就由江蘇公務(wù)員考試網(wǎng)小編帶領(lǐng)大家一起來學(xué)習(xí)解決均值不等式這類題型的方法，從而讓大家對這類題型有進(jìn)一步的認(rèn)識。
相關(guān)文章
一、均值不等式的含義：
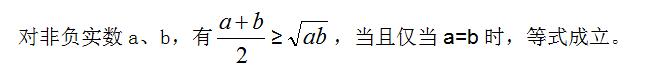
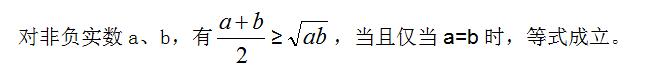
二、均值不等式的結(jié)論：
1、和一定，當(dāng)且僅當(dāng)兩數(shù)相等時，乘積最大;
2、積一定，當(dāng)且僅當(dāng)兩數(shù)相等時，和最小;
總結(jié)：和或積一定時，當(dāng)且僅當(dāng)兩數(shù)相等時有最值。
三、均值不等式的應(yīng)用
例4.建造一個容積為16立方米，深為4米的長方體無蓋水池，如果池底和池壁的造價分別為每平方米160元和每平方米100元，那么該水池的最低造價是多少元?
A.3980 B.3560 C.3270 D.3840
【答案】D。解析：若長方體無蓋水池底的邊長為a、b，則其面積a×b=16÷4=4，水池的最低造價為4×160+(a×4×2+b×4×2)×100=640+800×(a+b)，求最低造價，即求a+b的最小值，符合乘積一定，求和最小，當(dāng)且僅當(dāng)a=b= =2，則最低造價為640+800×(a+b)=640+800×(2+2)=3840，故選擇D選項。
通過上述四道例題，相信大家對于求解均值不等式的題目已經(jīng)有了進(jìn)一步的認(rèn)識。那么在接下來的練習(xí)中，希望大家能夠進(jìn)一步將求解均值不等式的方法應(yīng)用于實踐，最后祝愿大家考試順利!
« 上一篇
|
沒有了
相關(guān)文章
