一道題多種解法,方法知識一起學(xué)
幾何問題是行測考試常見的考點之一,江蘇公務(wù)員考試網(wǎng)通過深入剖析,讓大家了解這道題的多種解法,拓展思路,同時考生們也能學(xué)習(xí)一些幾何基本知識點,一舉兩得。
 相關(guān)文章
相關(guān)文章
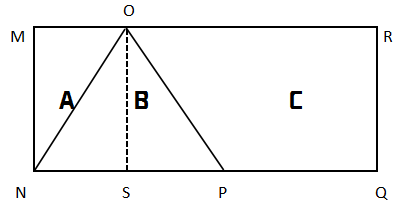
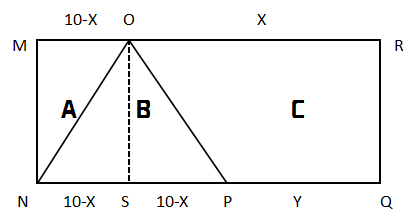
例題:將一塊長10厘米、寬4厘米的長方形平板切割成A、B、C共3塊,其中C塊的面積為22平方厘米,B為等腰三角形,那么A塊的面積是( )。

A.6平方厘米 B.12平方厘米 C.8平方厘米 D.4平方厘米
第一種方法:巧用兩種圖形的基本性質(zhì)
本題給出一個條件,即B是一個等腰直角三角形,等腰三角形有幾個基本性質(zhì),想必大家都比較熟悉,比如兩條腰相等;從兩腰之間的頂點往底邊作垂線,那此線就是三線合一,即垂直于底邊、平分頂角、平分底邊。如上圖,從O點做垂線OS,這條線把是三角形B分成兩個一樣的三角形,當(dāng)然這兩個三角形的面積肯定是相等的,在觀察四邊形MNSO構(gòu)成一個長方形,而ON正好是長方形的對角線,根據(jù)長方形的基本性質(zhì),對角線所分的兩個三角形大小相等,所以面積也相等,綜上可知,以上三個圖中左邊的三個三角形面積都相等,而已知大長方形面積為10×4=40,且C區(qū)域面積是22,所以剩下的三個三角形的區(qū)域是40-22=18,18÷3=6即是所求的三角形的面積。
這種方法費時最少,技巧性比較強(qiáng)。用到的幾何知識點有:等腰三角形“三線合一”的基本性質(zhì),長方形的對角線的性質(zhì),長方形的面積公式等知識點。
第二種方法:巧用三角形全等和方程法。
第二種方法相較于第一種方法計算的過程要相對復(fù)雜,但也是考生們的正常思考路徑。 從P點向RM邊作垂線。利用三角形NOP是等腰三角形的性質(zhì),可以證明三角形OMN和三角形OSP全等。怎么證明呢,已知這兩個三角形都是直角三角形,我們知道直角三角形有一個特殊的證明方法,簡稱“HL”,“H”是直角邊;在本題中指的是MN=SP,“L”是斜邊,指的是ON=OP。

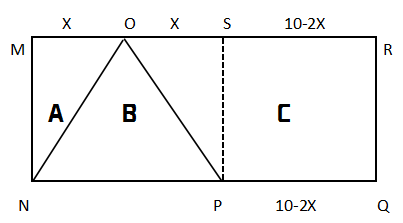
證明全等后,可以得到OM=OS。已知C區(qū)域是面積是22,C還是一個梯形。梯形的面積公式是:(上底+下底)×高÷2,可以設(shè)未知線段OS=OM為X,可以得到梯形的較長的底邊長為10-X,而SPQR構(gòu)成的是一個矩形,那SR=PQ=10-2X,PQ即為梯形較短的底邊。高已知是RQ=4,可列方程:(10-2X+10-X)×4÷2=22,解得X=3。那三角形A的面積就是4×3÷2=6。
本題所用到的知識點除了梯形的面積公式以外,還有:三角形全等的證明和邊長相等的性質(zhì)、矩形對應(yīng)邊相等的性質(zhì)。
第三種方法:巧用方程組和梯形公式

本題為了利用梯形公式,還可用方程的方法去做。
OR和PQ都是未知條件,分別設(shè)為X和Y,那OM=10-X,NS=SP=10-X,PQ=10-2×(10-X)=Y,化簡可得方程:2X-Y=10,又已知梯形面積為:(X+Y)×4÷2=22,化簡得X+Y=11,聯(lián)立兩個方程為方程組,解得x=7,OM=10-X=10-7=3,計算可得三角形A的面積為6。
此解法與以上兩種解法所用知識點部分重復(fù),不再一一列舉。
綜上可以看出,解某一道數(shù)學(xué)題的方法不止一種,需要諸位考生耐心去尋找;不同的方法所需的知識點可能相同,也可能需要新的知識點。所以需要考生擴(kuò)大知識面,做題不貪多,對于自己做過的題目要反復(fù)琢磨,讓自己得到實質(zhì)的提升。
 相關(guān)文章
相關(guān)文章