2016���K���ՆT��(sh��)�W�\�㿼�c����φ��}
����һ���������

 ���P(gu��n)����
���P(gu��n)����
�����ڽ��K���ՆT��ԇ���� ��(sh��)�W�\�㆖�}һ���֞�ʮ�Ă�ģ�K������һ�K�dz��ԭ�톖�}��

�����������ԭ������
�������ԭ�����ֽе�������ԭ��������һ����Ҫ���ֻ����Ĕ�(sh��)�Wԭ�������������Խ�Q���N��Ȥ�Ć��}�����ҳ����܉�õ������@��ĽY(ji��)�����S������ஔ���s�������o�����ֵĆ��}���������ܺ����õ���Q����ô��ʲô�dz��ԭ����?�҂��ȏ�һ����ε�����Մ��
�����������O���ŵ���ֻ���������һ�������ܕ���ʲô�ӵĽY(ji��)����?Ҫô��һֻ�����Ńɂ��O��������һֻ������һ���O��;Ҫôһֻ�������������O��������һֻ����ﲻ�š��@�ɷN��r����һ��Ԓ������һ����һֻ���������˃ɂ���ɂ����ϵ��O�����mȻ��ֻ�����������كɂ��O���҂��o���ඨ�����@�ǟo�P(gu��n)�oҪ������Ҫ�������@��һֻ��Ϸ����˃ɂ���ɂ����ϵ��O����
��������҂������憖�}��һ��׃�ӣ����粻�nj������O�������ֻ����������nj��˂��O���ŵ���ֻ��������҂����y�l(f��)�F(xi��n)���@�˂��O���oՓ�����ӵķ�ʽ����������Ȼһ������һֻ����������Ѓɂ��O����
�����ڹ��ՆT��ԇ��(sh��)�W�\������������ԭ�톖�}�r���}��ͨ����“����……�����ܱ��C……”�@�ӵ����ۡ�
�����҂������v��һ�³��ԭ���ăɂ���Ҫ�Y(ji��)Փ��
�����ٳ��ԭ��1
����������n������Ʒ����ŵ�n������У���ô������һ������е���Ʒ����(sh��)������2��(Ҳ���������������2����Ʒ��ͬһ�����)
�����ڳ��ԭ��2
����������m×n������Ʒ����ŵ�n�����������ô������һ������е���Ʒ�ļ���(sh��)������m+1��(Ҳ���������������m+1����Ʒ��ͬһ�����)
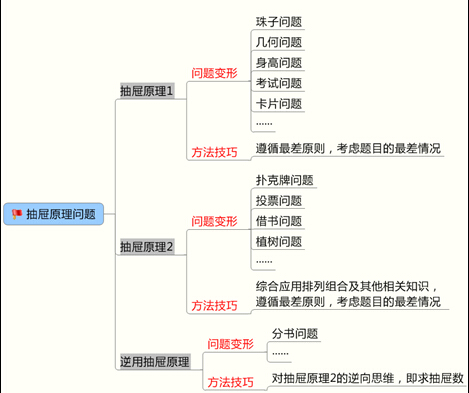
�������ՆT��ԇ�������ԭ�톖�}ͨ���c�������}��Y(ji��)�ρ��M�п�����һ��ֻ�г��ԭ��1�����ԭ��2�����ó��ԭ�����N���������ԭ�톖�}�ij��õķ�������ѭ���ԭ�t�������]�����r���䱾�|(zh��)���dz��ԭ�톖�}�Ļ���ԭ�����oՓ“���”��С���N���ô׃�������K���ՆT��ԇͨ�ý̲ľ����M���ώ����h����Ҫ���ΰ����@���N��ͺͽ��}ԭ�t�������p�ɸ㶨���ԭ�톖�}��

��������ֱ�����ó��ԭ�����}
����(һ)���ó��ԭ��1
�������}1����20λ�\�ӆT�����L���������ą�ِ̖�a�քe��1��2��3��…��20������Ҫ�����x�����ق���ِ̖�a�����ܱ��C�����Ѓɂ�̖�a�IJ���13�ı���(sh��)?
����A.12 B.15 C.14 D.13
����������������ʹ�ɂ�̖�a�IJ���13�����]���M���@���l���ăɂ���(sh��)����һ�M���@�ӵ�̖�a�քe��{1��14}��{2��15}��{3��16}��{4��17}��{5��18}��{6��19}��{7��20}����7�M��߀ʣ��̖�a8��9��10��11��12��13����6�������]������r����ȡ���@6��̖�a���ُ�ǰ7�M�е�ÿһ�Mȡ1��̖�a���@��������ȡ��1��̖�a���ܱ��C�����Ѓɂ�̖�a�IJ���13�ı���(sh��)����ȡ����6+7+1=14��̖�a��
����(��)���ó��ԭ��2
�������}2��һ���ڴ�����50������̖�a����ͬ��С�������о�̖��1��2��3��4��5�ĸ���10����һ������Ҫȡ������С�������ܱ��C����������4��̖�a��ͬ��С��?
����A.20�� B.25�� C.16�� D.30��
��������������1��2��3��4��5��N̖�a����5����ϡ�Ҫ���C��һ�������������4����Ʒ������(j��)���ԭ��2������Ҫȡ��5×3+1=16��С�������ܱ��C����������4��̖�a��ͬ��С����
�����ġ��������ԭ�t
�������ԭ�t�f�ľ����ڳ�φ��}��������������r����ô𰸡������ԭ�톖�}�������O����r���ʿ��ԏ�������r���]���ĸ���ՆT��ԇ���}������“���]�����r”�@һ������ʹ�ÏV��������Ч��
�������}3����һ�������ē�����������ٳ�����ُ��������ܱ��C����6���ƵĻ�ɫ��ͬ?
����A.21 B.22 C.23 D.24
������������һ�������ē���ư���������С��;�t�������K��������÷����13�����քe��A��2��3��4��5��6��7��8��9��10��J��Q��K��Ҫ��6���ƵĻ�ɫ��ͬ�����]�����r�����t�������K�����ҡ�÷�������5�����ټ��ϴ�����С�����˕r��ȡ����4×5+2=22�����˕r����ȡһ�����tһ����һ�N��ɫ������6����������ȡ��23���������ܱ��C����6���ƵĻ�ɫ��ͬ��
�������}4��һ���������д�С��ͬ���ɫ��ͬ��һЩС�������мt��10������9�����S��8�����{��2����һ������ȡ���ق��������ܱ��C��4����ͬ�ɫ����?
����A.12 B.13 C.14 D.15
����������������ĵ���r���]���t���ס��S���N�ɫ�����ȡ��3�����{ɫ����ȡ��2�����@�r��ȡ��3×3+2=11��������ȡ1��������ô����ȡ���ηN�ɫ���������ܱ��C��4����ͬ�ɫ������������Ҫȡ12����
�����塢�c���нM�φ��}�Y(ji��)��
�������}5��ij�^(q��)Ҫ��10λ���x����ͶƱ�x�e�˴�������F(xi��n)Ҏ(gu��)��ÿλ�x�e�˱�횏��@10λ�����x��λͶƱ��������Ҫ�ж���λ�x�e�˅���ͶƱ�����ܱ��C�в�����10λ�x�e��Ͷ����ͬ��λ���x�˵�Ʊ?
����A.382 B.406 C.451 D.516
��������������10λ���x�����x2�˹���C =45�N��ͬ���x����ÿ�N��ͬ���x������һ����ϡ�Ҫ���C�в�����10λ�x�e��Ͷ����ͬ��λ���x�˵�Ʊ���ɳ��ԭ��2֪������Ҫ��45×9+1=406λ�x�e��ͶƱ��
���������c�Ά��}�Y(ji��)��
�������}6����һ���L4������3���L����������������5������5�����о��x��С�ăɂ������x�����ֵ�Ƕ�����?
����A.5 B.4 C.3 D.2.5
���������������L���ηֳ��Ă�ȫ�ȵ�С�L����(�L��2��������1.5��)������5������Ԓ���t����2��������ͬһ��С�L�����У�����֮�g�ľ��x������С�L���Ό��Ǿ��L�����5�����о��x��С�ăɂ������x�����ֵ��2.5����
������x���ĵ���߀��x�ˣ�
 ���P(gu��n)����
���P(gu��n)����